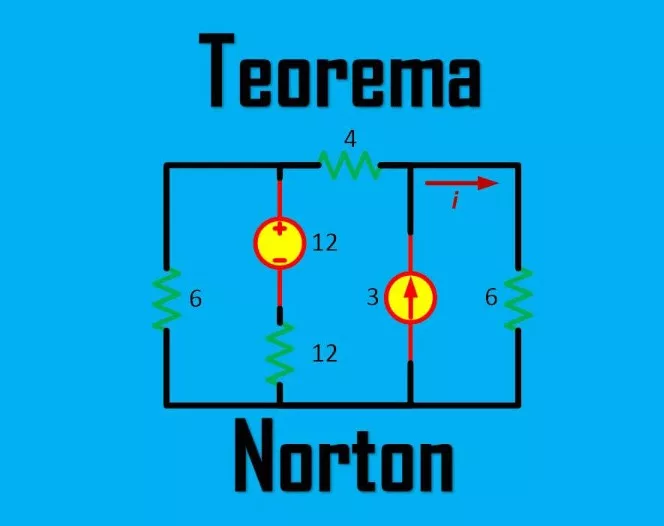
Empat Pilar – Pengertian Teorema Norton : Contoh Soal dan Cara Menghitung. Pengertian Teorema Norton, contoh soal, dan cara menghitungnya, sekaligus penjelasan mendalam untuk membantu Kalian memahami konsep penting dalam dunia teknik elektro.
Berbicara tentang hukum-hukum dan teori dalam ilmu fisika, khususnya dalam bidang teknik elektro, mungkin dapat membuat kepala Kalian pusing.
Namun, tidak ada yang perlu ditakuti ketika kita mengenal mereka lebih dekat. Salah satunya adalah Teorema Norton. Dalam artikel ini, kita akan mendalami Pengertian Teorema Norton: Contoh Soal dan Cara Menghitung.
Theorema Norton adalah sebuah teori dalam rangkaian listrik yang menyatakan bahwa setiap rangkaian listrik dapat digantikan dengan sumber arus dan hambatan paralel. Mungkin terdengar cukup sederhana, tapi mari kita menggali lebih dalam.
Teorema Norton dinamakan dari insinyur Amerika, Edward Lawry Norton. Teorema ini sangat penting dalam analisis rangkaian listrik, karena mempermudah proses perhitungan.
Teorema Norton juga dapat mempersingkat waktu analisis rangkaian yang kompleks, dan memungkinkan insinyur untuk lebih mudah memahami dan memanipulasi rangkaian listrik.
Pengertian Teorema Norton
Teorema Norton adalah salah satu teori atau alat analisis yang dapat digunakan untuk menyederhanakan rangkaian linear yang rumit menjadi rangkaian yang lebih sederhana.
Berbeda dengan Teorema Thevenin yang menggunakan sumber tegangan (Voltage Source) ekivalen dengan merangkai resistor ekivalen secara seri, Teorema Norton menyederhanakan rangkaian dengan menggunakan sumber arus (Current Source) ekivalen dan resistor ekivalen yang disusun secara paralel.
Teorema Norton ini ditemukan oleh dua peneliti, yaitu Hans Ferdinand Mayer dari Siemens & Halske dan Edward Lawry Norton dari Bell Labs. Oleh karena itu, sering juga disebut sebagai Teorema Mayer-Norton (Mayer-Norton Theorem).
Bunyi Teorema Norton
Berikut ini merupakan bunyi dari teorema norton, yaitu :
Setiap rangkaian listrik linear atau rangkaian yang kompleks dapat digantikan oleh sebuah rangkaian yang lebih sederhana yang terdiri dari sumber arus (IN) dan resistor yang disusun secara paralel (RN)
Rangkaian pengganti ini juga dikenal sebagai Rangkaian Norton Ekivalen.
Tujuan Teori Teorema Norton
Setelah memahami Pengertian Teorema Norton, selanjutnya tujuan dari Teorema Norton adalah:
1. Menyederhanakan Rangkaian
Teorema Norton digunakan untuk menyederhanakan rangkaian listrik yang kompleks menjadi bentuk yang lebih sederhana.
Dengan menggunakan rangkaian Norton, kita dapat menggantikan rangkaian yang rumit dengan sumber arus dan resistor paralel yang lebih mudah dianalisis.
2. Analisis dan Perhitungan yang Lebih Mudah
Dengan menerapkan Teorema Norton, analisis dan perhitungan dalam rangkaian listrik menjadi lebih mudah.
Rangkaian yang kompleks dapat diubah menjadi rangkaian Norton yang lebih sederhana, yang mempermudah penghitungan arus dan tegangan dalam rangkaian tersebut.
3. Penggantian Sirkuit
Teorema Norton memungkinkan penggantian sirkuit yang rumit dengan sumber arus dan resistor paralel yang ekivalen.
Hal ini memudahkan dalam perancangan dan pemodelan sirkuit elektronik yang kompleks dengan menggunakan rangkaian yang lebih sederhana.
4. Memahami Karakteristik Rangkaian
Dengan menggunakan Teorema Norton, kita dapat memahami karakteristik penting dari suatu rangkaian, seperti resistansi ekivalen dan arus sirkuit. Hal ini membantu dalam analisis dan desain rangkaian elektronik dengan lebih baik.
Cara Menganalisis Rangkaian Linear dengan Perhitungan Teorema Norton
Berikut adalah langkah-langkah untuk menganalisis dan menghitung rangkaian linear menggunakan Teorema Norton:
- Hubungkan resistor beban secara singkat.
- Hitung atau ukur arus pada rangkaian yang disingkat. Arus ini disebut Arus Norton (IN).
- Matikan sumber arus, singkat sumber tegangan, dan lepaskan resistor beban.
- Hitung atau ukur resistansi rangkaian yang terbuka. Resistansi ini disebut Resistansi Norton (RN).
- Gambarkan ulang rangkaian dengan memasukkan nilai arus dari langkah 2 ke dalam rangkaian yang disingkat.
- Hubungkan arus sumber dan resistor yang terbuka pada rangkaian secara paralel.
- Sambungkan kembali resistor beban yang sebelumnya dilepas pada langkah 3.
- Ini adalah rangkaian yang disederhanakan menggunakan Teorema Norton, juga dikenal sebagai rangkaian Norton Ekivalen.
- Temukan arus beban yang mengalir dan tegangan beban pada resistor beban menggunakan aturan pembagi arus listrik (Current Divider Rule).
IL = IN / (RN/(RN+RL))
Dengan mengikuti langkah-langkah di atas, kita dapat menganalisis dan menghitung rangkaian linear menggunakan perhitungan Teorema Norton.
Rumus Arus Teori Teorema Norton
Rumus Arus Teori Teorema norton tujuannya adalah untuk mendapatkan rangkaian ekuivalen dengan sumber arus yang terdapat paralel. Nah, paralel ini terdapat resistansi ekivalen.
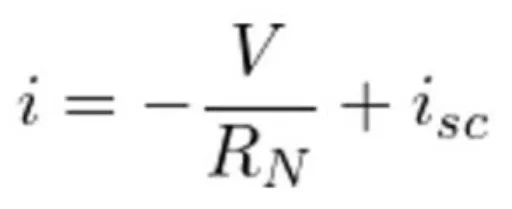
Cara Menghitung Teori Teorema Norton dengan Rumus
Setelah membahas Pengertian Teorema Norton, nah selanjutnya cara menghitung Teorema Norton sebenarnya bisa dilakukan dengan sangat sederhana. Hal ini karena Kalian dapat menggunakan rumus dari Teorema Thevenin untuk mencari rangkaian ekivalen Norton.
Pertama, gunakan rumus resistansi ekivalen Thevenin (RTh) karena ekivalen ini setara dengan rangkaian linier. Rumus RTh tidak melibatkan hubungan antara tegangan dan arus.
Kedua, gunakan rumus RN atau resistansi ekivalen Norton untuk menghitung rangkaian Norton.
1. Cara Menghitung Rumus Nilai Resistansi Ekivalen Norton
Rumus untuk menghitung nilai Resistansi Ekivalen Norton adalah sebagai berikut:
RN = RTh
2. Cara Menghitung Rumus Arus Short Circuit
Sebelum mengetahui hasil Arus Ekuivalen Norton (IN), kita perlu menghitung arus yang melalui terminal short circuit a-b. Rumusnya adalah sebagai berikut:
IN = iSC
3. Cara Menghitung Rumus Transformasi Sumber
Teorema Norton-Thevenin dapat diterapkan pada sumber bebas dan tidak bebas dengan cara yang sama. VTh1, IN1, dan RTh saling berhubungan, membentuk teorema transformasi sumber. Secara singkat, penjelasannya adalah sebagai berikut:
- Open circuit dan short circuit pada terminal a-b menghasilkan Voc (tegangan open circuit) dan iSC (arus short circuit).
- Resistansi ekivalen pada terminal a-b, karena RN merupakan sumber bebas yang dinonaktifkan.
- Berikut adalah contoh rumusnya:
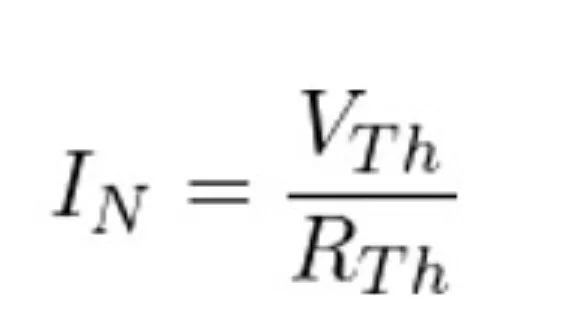
4. Cara Menghitung Rumus Hukum Ohm Dasar
Dalam menghitung Teorema Norton, kita menggunakan hukum Ohm dasar. Berikut adalah rumus-rumus yang terkait dengan Teorema Norton:
VTh = Voc
IN = isc
RTh = Voc / isc = RN
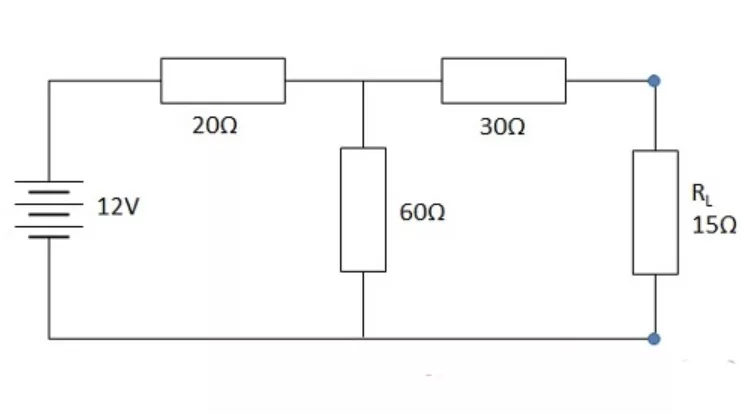
Contoh Soal Perhitungan Teorema Norton
Ketika sudah memahami Pengertian Teorema Norton, Lalu berikutnya adalah contoh soal mengenai perhitungan teorema Norton yang dapat Anda pelajari. Meskipun pada pandangan pertama rangkaian Thevenin dan Norton terlihat serupa, sebenarnya terdapat beberapa perbedaan di antara keduanya.
Soal:
Sebuah rangkaian memiliki resistor beban sebesar 17 Ω, dengan resistor paralel 80 Ω dan 60 Ω, yang terhubung dengan sebuah resistor seri 40 Ω. Tegangan yang terjadi di rangkaian tersebut adalah 16 V.
Berapakah resistansi Norton (RN), arus Norton (IN), resistansi beban, dan tegangan beban (VL) berdasarkan teorema Norton? Gunakan rumus teorema Norton yang tepat!
Diketahui:
RB = 17 Ω
R1 = 80 Ω
R2 = 60 Ω
R3 = 40 Ω
Ditanya:
Resistansi Norton (RN)
Arus Norton (IN)
Resistansi Beban
Tegangan Beban (VL)
Jawab:
1. Langkah pertama, singkatkan resistor beban 17 Ω. Cari total resistansi (Rt) sebagai berikut:
Rt = 40 + [(80 x 60) / (80 + 60)]
Rt = 40 + 4800/140
Rt = 40 + 34.2857
Rt = 74.2857 Ω (diaproximasi menjadi 74 Ω)
2. Selanjutnya, cari total arus listrik (It) sebagai berikut:
It = RB / Rt
It = 17 / 74
It = 0.2297 A (diaproximasi menjadi 0.23 A)
3. Selanjutnya, cari arus Norton (IN) sebagai berikut:
IN = It x (Rt / (Rt + R3))
IN = 0.23 x (74 / (74 + 40))
IN = 0.23 x 0.648
IN = 0.14904 A (diaproximasi menjadi 0.149 A)
Dengan melakukan singkatan pada resistor beban, salah satu rangkaian menjadi terbuka. Teorema Norton dianalisis berdasarkan konsep arus linear, sehingga diperlukan nilai resistansi rangkaian tersebut, yaitu RN.
4. Selanjutnya, cari resistansi Norton (RN) sebagai berikut:
RN = R2 + [(R1 x R3) / (R1 + R3)]
RN = 60 + [(80 x 40) / (80 + 40)]
RN = 60 + 3200/120
RN = 60 + 26.6667
RN = 86.6667 Ω (diaproximasi menjadi 87 Ω)
5. Setelah itu, hitung arus beban sebelum menghitung tegangan beban (VL) sebagai berikut:
IL = IN x (RN / (RN + RB))
IL = 0.149 x (87 / (87 + 17))
IL = 0.149 x 0.8372
IL = 0.1249 A (diaproximasi menjadi 0.125 A)
6. Terakhir, hitung tegangan beban (VL) sebagai berikut:
VL = IL x RB
VL = 0.125 x 17
VL = 2.125 V (diaproximasi menjadi
Penutup
Dalam artikel ini, kita telah membahas secara mendalam tentang pengertian Teorema Norton, berbagai contoh soal, serta langkah-langkah untuk menghitungnya.
Pengetahuan tentang Teorema Norton merupakan hal yang penting dalam bidang elektronika dan teknik listrik.
Semoga penjelasan, contoh soal dan cara menghitung yang telah dijelaskan dalam artikel ini, membantu Kalian dalam memahami dan menerapkan Teorema Norton dalam kehidupan sehari-hari maupun dalam studi Kalian.
Ingatlah bahwa praktek adalah kunci untuk memahami konsep yang kompleks seperti Teorema Norton.
Jadi, berlatihlah sebanyak mungkin dengan berbagai jenis soal agar Kalian semakin menguasai materi ini.
Semoga artikel dari empatpilar.com ini, menjadi panduan yang berguna dan dapat memberikan pencerahan dalam pemahaman Kalian tentang Pengertian Teorema Norton.
Teruslah belajar dan tetap semangat dalam menghadapi setiap tantangan belajar yang datang. Kata Pencarian Terpopulerhttps://www empatpilar com/pengertian-teorema-norton/